DBSCAN¶
Density-based Spatial Clustering of Applications with Noise (DBSCAN) is a data clustering algorithm that finds clusters through density-based expansion of seed points. The algorithm is proposed by:
Martin Ester, Hans-peter Kriegel, Jörg S, and Xiaowei Xu A density-based algorithm for discovering clusters in large spatial databases with noise. 1996.
Density Reachability
DBSCAN’s definition of cluster is based on the concept of density reachability: a point 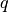 is said to be directly density reachable by another point
is said to be directly density reachable by another point  if the distance between them is below a specified threshold
if the distance between them is below a specified threshold  and
and  is surrounded by sufficiently many points. Then,
is surrounded by sufficiently many points. Then, 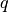 is considered to be density reachable by
is considered to be density reachable by  if there exists a sequence
if there exists a sequence 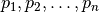 such that
such that 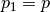 and
and 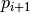 is directly density reachable from
is directly density reachable from 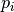 .
.
A cluster, which is a subset of the given set of points, satisfies two properties:
- All points within the cluster are mutually density-connected, meaning that for any two distinct points
 and
and 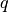 in a cluster, there exists a point
in a cluster, there exists a point  sucht that both
sucht that both  and
and 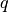 are density reachable from
are density reachable from  .
. - If a point is density connected to any point of a cluster, it is also part of the cluster.
Functions
There are two different implementations of DBSCAN algorithm called by dbscan function in this package:
- Using a distance (adjacency) matrix and is O(N^2) in memory usage. Note that the boundary points are not unique.
-
dbscan(D, eps, minpts) Perform DBSCAN algorithm based on a given distance matrix.
Parameters: - D – The pairwise distance matrix.
D[i,j]is the distance between pointsiandj. - eps – The radius of a neighborhood.
- minpts – The minimum number of neighboring points (including self) to qualify a point as a density point.
The algorithm returns an instance of
DbscanResult, defined as below:type DbscanResult <: ClusteringResult seeds::Vector{Int} # starting points of clusters, size (k,) assignments::Vector{Int} # assignments, size (n,) counts::Vector{Int} # number of points in each cluster, size (k,) end
- D – The pairwise distance matrix.
2. Using an adjacency list which is build on the fly. The performance is much better both in terms of runtime and memory usage. Also, the result is given in a DbscanCluster that provides the indices of all the core points and boundary points, such that boundary points can be associated with multiple clusters.
-
dbscan(points, radius, leafsize=20, min_neighbors=1, min_cluster_size=1) Perform DBSCAN algorithm based on a collection of points.
Parameters: - points – matrix of points (column based)
- radius – The radius of a neighborhood.
- leafsize – number of points binned in each leaf node in the KDTree
- min_neighbors – minimum number of neighbors to be a core point
- min_cluster_size – minimum number of points to be a valid cluster
The algorithm returns an instance of
DbscanCluster, defined as below:- immutable DbscanCluster <: ClusteringResult
- size::Int # number of points in cluster core_indices::Vector{Int} # core points indices boundary_indices::Vector{Int} # boundary points indices
end