Silhouettes¶

Silhouettes is a method for validating clusters of data. Particularly, it provides a quantitative way to measure how well each item lies within its cluster as opposed to others. The Silhouette value of a data point is defined as:

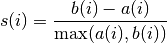
$s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$

Here, 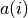$a(i)$ is the average distance from the i-th point to other points within the same cluster. Let 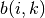$b(i, k)$ be the average distance from the i-th point to the points in the k-th cluster. Then 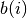$b(i)$ is the minimum of all 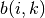$b(i, k)$ over all clusters that the i-th point is not assigned to.

Note that the value of 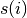$s(i)$ is not greater than one, and that 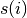$s(i)$ is close to one indicates that the i-th point lies well within its own cluster.

silhouettes(assignments, counts, dists)

Compute silhouette values for individual points w.r.t. a given clustering.

Parameters:	assignments – the vector of assignments counts – the number of points falling in each cluster dists – the pairwise distance matrix
Returns:	It returns a vector of silhouette values for individual points. In practice, one may use the average of these silhouette values to assess given clustering results.

silhouettes(R, dists)

This method accepts a clustering result R (of a sub-type of ClusteringResult).

It is equivalent to silhouettes(assignments(R), counts(R), dists).