K-means

K-means is a classic method for clustering or vector quantization. The K-means algorithms produces a fixed number of clusters, each associated with a center (also known as a prototype), and each sample belongs to a cluster with the nearest center.

From a mathematical standpoint, K-means is a coordinate descent algorithm to solve the following optimization problem:

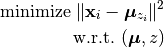
Here, 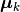is the center of the k-th cluster, and 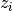indicates the cluster for .

This package implements the K-means algorithm in the kmeans function:

kmeans(X, k; ...)

Performs K-means clustering over the given dataset.

Parameters:

• X – The given sample matrix. Each column of X is a sample.
• k – The number of clusters.

This function returns an instance of KmeansResult, which is defined as follows:

type KmeansResult{T<:FloatingPoint} <: ClusteringResult
    centers::Matrix{T}         # cluster centers, size (d, k)
    assignments::Vector{Int}   # assignments, length n
    costs::Vector{T}           # costs of the resultant assignments, length n
    counts::Vector{Int}        # number of samples assigned to each cluster, length k
    cweights::Vector{Float64}  # cluster weights, length k
    totalcost::Float64         # total cost (i.e. objective)
    iterations::Int            # number of elapsed iterations
    converged::Bool            # whether the procedure converged
end

One may optionally specify some of the options through keyword arguments to control the algorithm:

name	description	default
init	Initialization algorithm or initial seeds, which can be either of the following: a symbol indicating the name of seeding algorithm, :rand, :kmpp, or :kmcen (see Clustering Initialization) an integer vector of length k that provides the indexes of initial seeds.	:kmpp
maxiter	Maximum number of iterations.	100
tol	Tolerable change of objective at convergence.	1.0e-6
weights	The weights of samples, which can be either of: nothing: each sample has a unit weight. a vector of length n that gives the sample weights.	nothing
display	The level of information to be displayed. (see Common Options)	:none

If you already have a set of initial center vectors, you may use kmeans! instead:

kmeans!(X, centers; ...)

Performs K-means given initial centers, and updates the centers inplace.

Parameters:

• X – The given sample matrix. Each column of X is a sample.
• centers – The matrix of centers. Each column of centers is a center vector for a cluster.

Note: The number of clusters k is determined as size(centers, 2).

Like kmeans, this function returns an instance of KmeansResult.

This function accepts all keyword arguments listed above for kmeans (except init).

Examples:

using Clustering

# make a random dataset with 1000 points
# each point is a 5-dimensional vector
X = rand(5, 1000)

# performs K-means over X, trying to group them into 20 clusters
# set maximum number of iterations to 200
# set display to :iter, so it shows progressive info at each iteration
R = kmeans(X, 20; maxiter=200, display=:iter)

# the number of resultant clusters should be 20
@assert nclusters(R) == 20

# obtain the resultant assignments
# a[i] indicates which cluster the i-th sample is assigned to
a = assignments(R)

# obtain the number of samples in each cluster
# c[k] is the number of samples assigned to the k-th cluster
c = counts(R)

# get the centers (i.e. mean vectors)
# M is a matrix of size (5, 20)
# M[:,k] is the mean vector of the k-th cluster
M = R.centers

Example with plot

using RDatasets

iris = dataset("datasets", "iris")
head(iris)

# K-means Clustering unsupervised machine learning example

using Clustering

features = permutedims(convert(Array, iris[:,1:4]), [2, 1])   # use matrix() on Julia v0.2
result = kmeans( features, 3 )                                # onto 3 clusters

using Gadfly

plot(iris, x = "PetalLength", y = "PetalWidth", color = result.assignments, Geom.point)